Huffman Coding

A simple Huffman Code

First, we’ll put the items in order of decending probabilities (smallest probs to the right).

Then, there are 3 repeatable steps to creating the binary tree that determines your Huffman Code:

1. find the two items with the lowest probabilities p_i and p_j
2. connect the two items
3. add their probabilities together, and treat them as a new node with probability p_i + p_j

note: if there’s a tie, where it’s not clear which two probabilities to pick, like here where we have all probabilities equal to 0.25, take the two rightmost items, it’ll make a cleaner tree.

We’ll keep doing steps 1-3 until we’ve covered all the items we have.

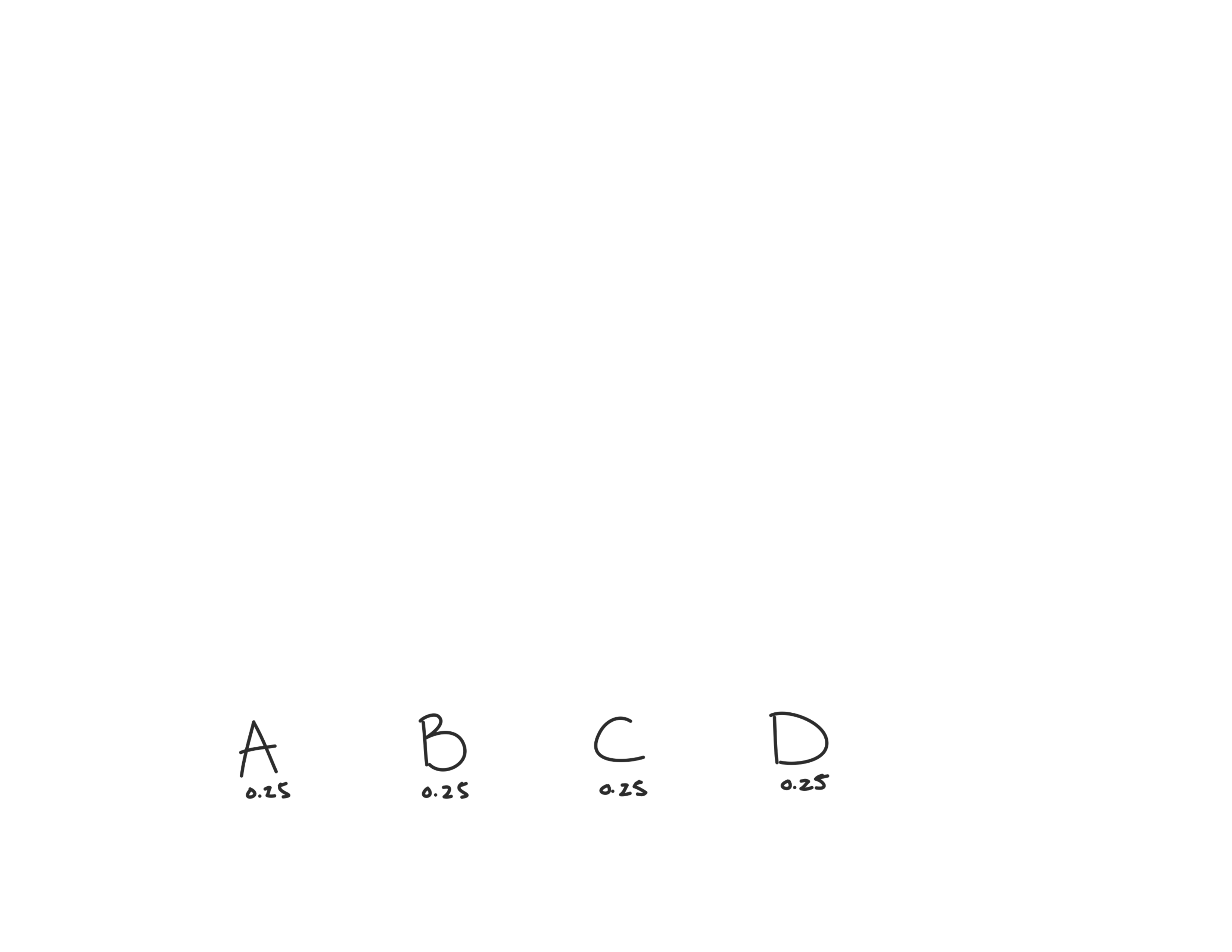
Since all our probabilities are the same, we’ll first combine the two rightmost ones: C and D.

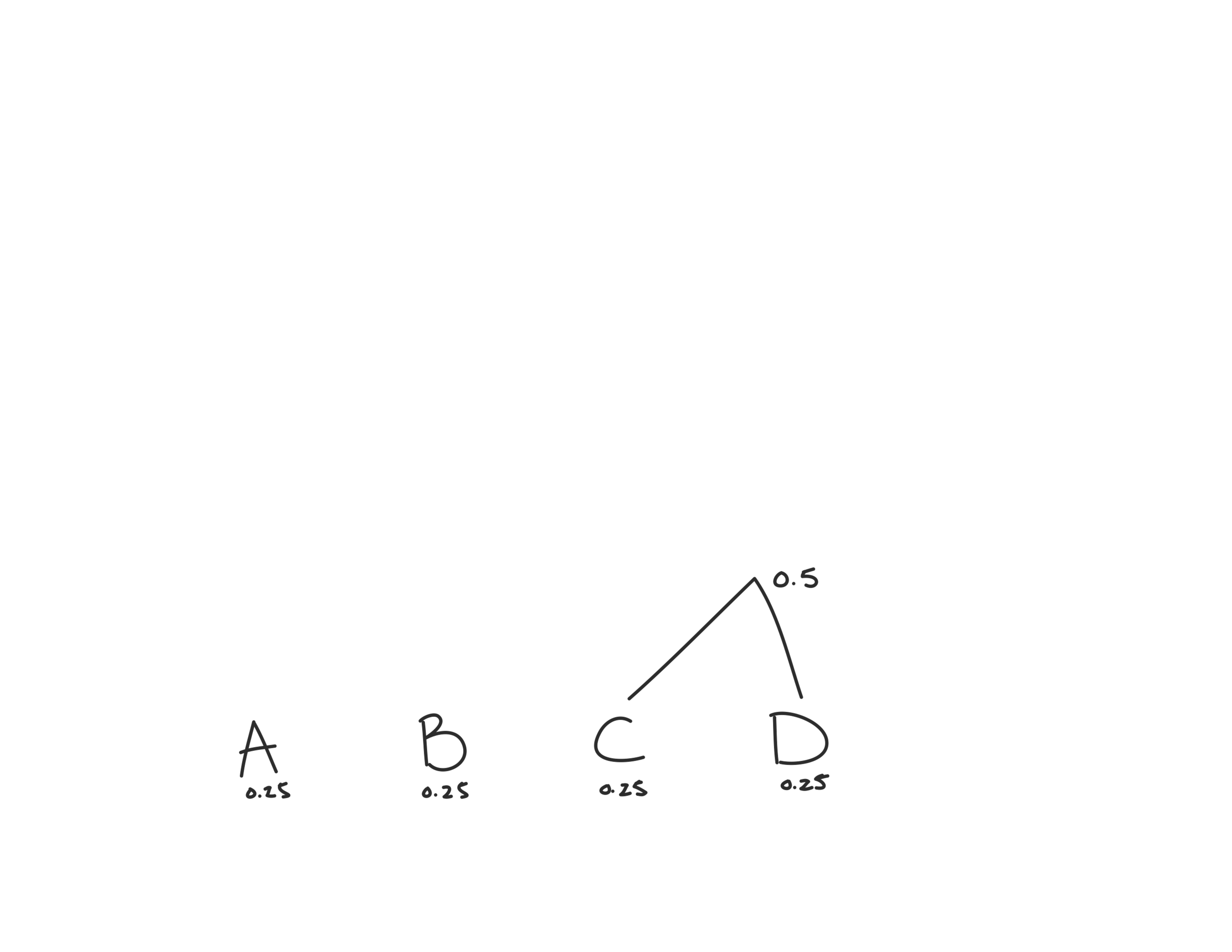
Now we have three probabilities to consider: 0.25, 0.25 and 0.5. We’ll combine the two lowest: A and B.

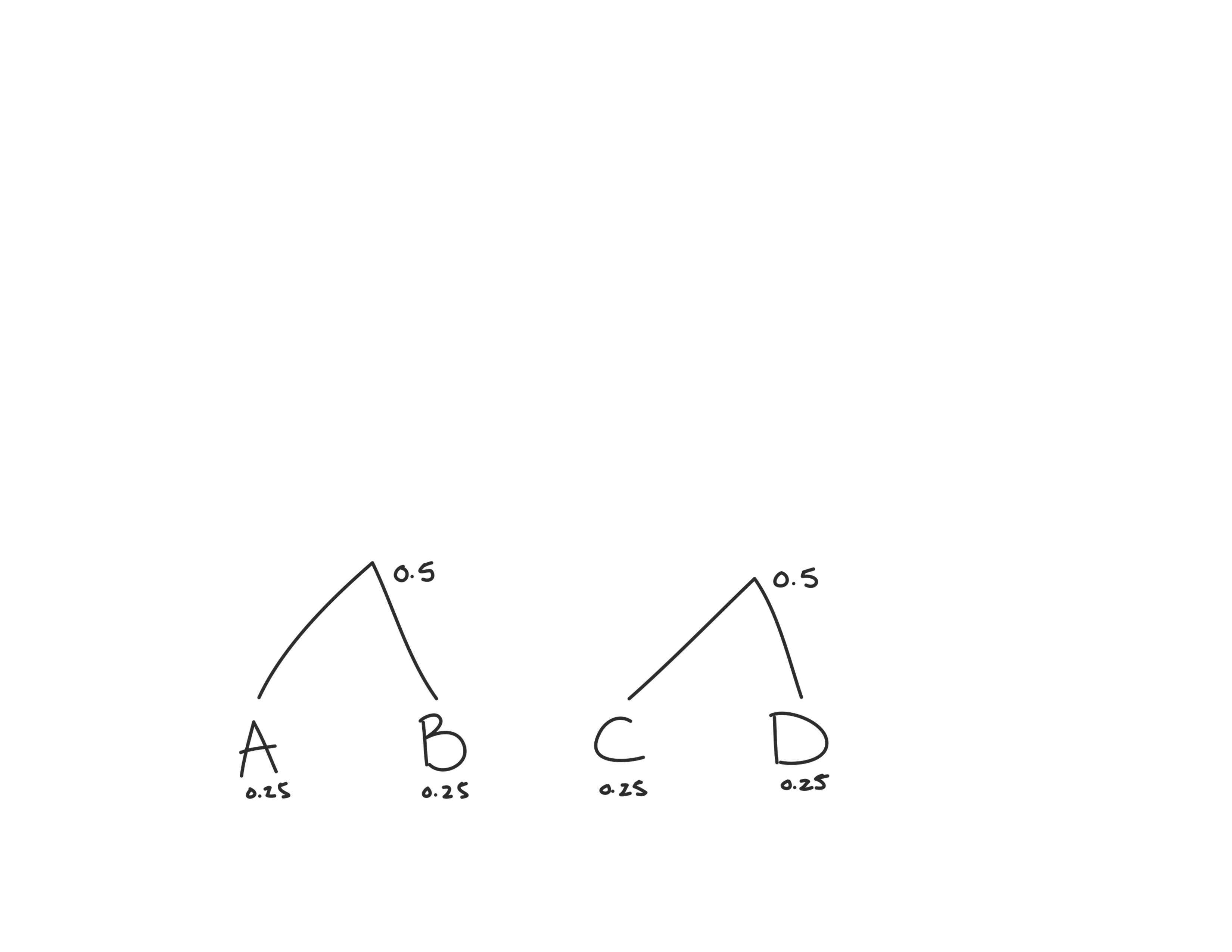
Now there’s only two left, so we’ll combine our two 0.5s to create the root node that has probability 1.

To create our code from this binary tree, we’ll start at the root and use a 0 every time we take the right path, and 1 every time we take the left.

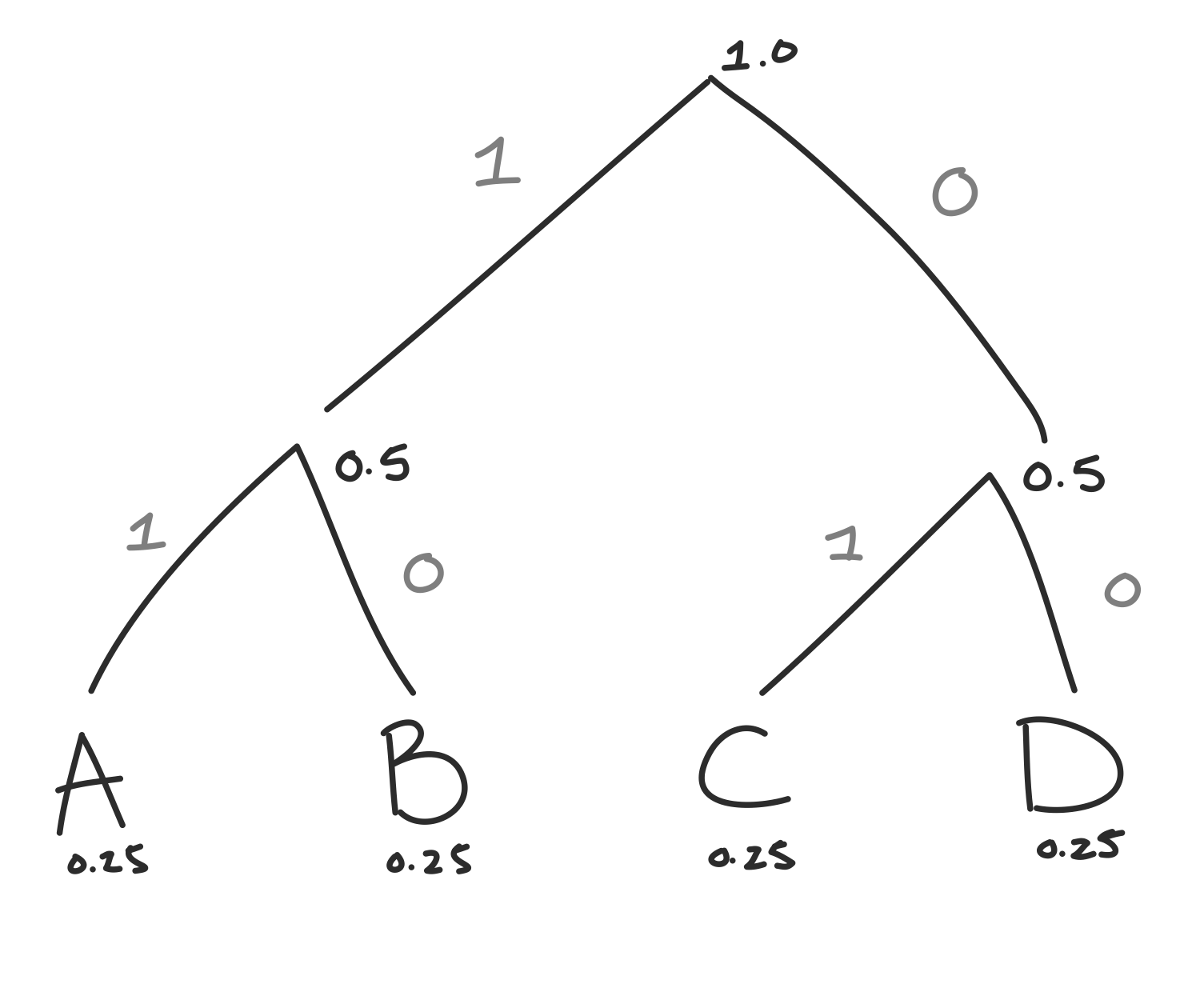
To get the code for each answer, we’ll just follow the tree down. For example to get to A we go left, left so the code for A will be 11 (or tap tap).

What a coincidence!! We just created the same code we originally used. Since Huffman Coding guarentees that the most efficient code, it looks like in this case we can’t improve the efficiency of our coughs and taps.

A more useful Huffman Code

Let’s try again, this time incorperating the information that your teacher, whose name is Brian, uses the answer B 50% of the time, A 10% of the time, C 20% of the time, and D 20% of the time. Now let’s create a new Huffman Code.

This time the binary codes for A,B,C and D are:

A: 000
B: 1
C: 01
D: 001

Now our codes are looking different. The codes are also different lengths. B is just 1, whereas A is 000. Huffman Coding takes advantage of the fact that B occurs the most, whereas A occurs the least. The way we’ve coded our letters, the ones that occur the most have the shortest codes. This will lead to a lower number of average bits to transcribe the answers to your friend’s test.

Previously, our code had an average of 2 bits per letter. We got that using this formula:

\[\sum\limits_{k = 1}^K p(k) log_2(k)\]

Where \(log_2(k)\) is the number of bits needed to code each letter.

In our new encoding we get \(0.5(1) + 0.2(2) + 0.2(3) + 0.1(3) = 1.8\). Before we needed an average of 2 bits to relay the test answers, but now that we’ve taken advantage of the fact that Brian likes B’s and not A’s we’ve reduced the average number of bits down to 1.8. While that’s not a huge improvement, if your friend’s test is 50 questions long, it saves you 10 coughs/taps, which certainly will make things a bit easier!